الگوریتم‌های پیداکردن ریشه

مقدمه

اساساً الگوریتم پیدا کردن ریشه یا ریشه‌یابی، یک الگوریتم برای پیدا کردن ریشه‌های توابع پیوسته‌است.

یک ریشه از تابع ${\begin{alignedat}{2}f\end{alignedat}}$ هنگامی پیدا می‌شود که ${\displaystyle {\begin{alignedat}{2}x\end{alignedat}}}$ در معادلهٔ ${\displaystyle {\begin{alignedat}{2}f(x)=0\end{alignedat}}}$ صدق کند و به آن x ریشهٔ تابع ${\begin{alignedat}{2}f\end{alignedat}}$می‌گوییم یا در معادلهٔ زیر هنگامی ریشهٔ ${\begin{alignedat}{2}f\end{alignedat}}$را پیدا می‌کنیم که حاصل تفریق دو تابع دیگر برابر ۰ شود.

${\begin{alignedat}{2}f(x)&=g(x)-h(x)\\&=>g(x)-f(x)=0\\&=>g(x)=f(x)\end{alignedat}}$

به‌طور کلی ریشه‌های بسیاری از توابع را نمی‌توان به صورت دقیق محاسبه کرد و الگوریتم پیدا کردن ریشه (Root-finding algorithm)به ما کمک می‌کند که به صورت تقریبی آنها را محاسبه کنیم.

اکثر الگوریتم‌های ریشه‌یابی با استفاده از انتخاب دنباله‌ای از اعداد امیدوارند که این دنباله به عنوان یک حد به سمت ریشه همگرایی داشته باشد. آنها با استفاده از یک یا چند حدس اولیه از ریشه، به عنوان مقادیر شروع می‌کنند سپس هر تکرار الگوریتم تقریب بهتری از ریشه را برای ما به ارمغان می‌آورد.

روش‌های براکتی (Bracketing methods)

در این گونه روش‌ها با تعیین بازه‌های کوچک و استفاده از آنها در برخی فرمول‌ها سعی می‌کنیم که به ریشه دست پیدا کنیم.

روش تنصیف یا دو بخشی

این روش از ساده‌ترین و قابل اعتمادترین روش‌های تکراری برای حل معادلهٔ غیر خطی است. این روش همچنین به عنوان روش تقسیم باینری(binary chopping) یا نیمه بازه(half-interval method)نیز شناخته می‌شود.

در این روش تابع ${\begin{alignedat}{2}f\end{alignedat}}$را به $n$بازهٔ مختلف $[a,b]$تقسیم می‌کنیم تا ریشه‌ای مانند $\epsilon$را پیدا کنیم بدین صورت که:$$if\quad (f({(a_{n}+b_{n}) \over 2})=0)\quad then\quad \epsilon ={(a_{n}+b_{n}) \over 2}$$$$if\quad (f(a_{n})f({(a_{n}+b_{n}) \over 2})<0)\quad then\quad set\quad a_{n+1}=a_{n}\ \ ;\ \ b_{n+1}={(a_{n}+b_{n}) \over 2}$$در غیر این صورت:$$seta_{n+1}={\frac {a_{n}+b_{n}}{2}}\quad ;\quad b_{n+1}=b_{n}$$برای فهم بهتر به تصویر زیر توجه کنید:

روش نابجایی

در این روش مانند روش قبل تابع مورد نظر را بازه بازه می‌کنیم ولی در این روش سریع تر به این مسئله و رسیدن به ریشه اهمیت می‌دهیم. بدین صورت که:$$w={{(\ \ f(b_{i-1})\ a_{i-1}-f(a_{i-1})\ b_{i-1}\ )} \over f(b_{i-1})-f(a_{i-1})}$$$$if\ (f(a_{n})f(w)\leqslant 0)\quad then\ set\ a_{n+1}=a_{n}\ ;\ b_{n+1}=w$$در غیر این صورت$$a_{n+1}=w\ ;\ b_{n+1}=b_{n}$$برای درک بهتر به تصویر زیر توجه کنید:

regula falsi

روش تعامل (Interpolation)

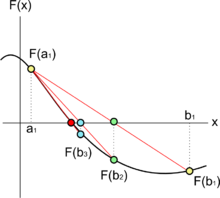
بسیاری از روش‌های پیدا کردن ریشه از این روش استفاده می‌کنند. این روش شامل استفاده از آخرین مقادیر تقریبی محاسبات ریشه برای تقریب تابع توسط یک چندجمله‌ای از درجه پایین است که مقادیر مشابهی را در این ریشه‌های تقریبی می‌گیرد.

سپس ریشهٔ چند جمله ای محاسبه می‌شود و به عنوان یک مقدار تقریبی جدید از ریشه تابع استفاده می‌شود و روند آن تکرار می‌شود.

دو مقدار به ما این امکان را می‌دهد که تابع را با یک چند جمله‌ای درجه یک تطبیق دهیم و سه مقدار یک چند جمله ای درجه دوم را درست می‌کند که گراف تابع را به وسیلهٔ یک سهمی تقریب می‌زند.

و این روش، روش مولر است.

روش‌های Iterative

با وجود اینکه تمام الگوریتم‌های ریشه‌یابی، به وسیلهٔ تکرار ادامه می‌یابند، یک روش Iterative، معمولاً از تکرار خاصی استفاده می‌کند که شامل تعریف یک تابع کمکی است که برای تقریب جدیدی به آخرین تقریب محاسبات یک ریشه اعمال می‌شود.

روش نیوتن

این روش مبتنی بر مشتقات تکراری است؛ بدین منظور که روش نیوتن فرض می‌کند که تابع f یک مشتق مداوم داشته باشد. اگر با استفاده از روش نیوتن مشتقات شروع به دور شدن از ریشه کند روش نیوتن همگرا نیست و این بدین معناست که از ریشه در حال دور شدن هستیم ولی هنگامی که همگرا می‌شود یعنی در حال نزدیک شدن به ریشه هستیم، این روش معمولاً از روش تنصیف بهتر و سریع تر است. روش نیوتن نیز مهم است زیرا به راحتی به مشکلات بزرگتر پاسخ می‌دهد. روش‌های نیوتن مانند با دستورات بالاتر از همگرایی روش‌های خانه‌دار(Householder's methods) است.

به عبارت دیگر در این روش ابتدا مشتق تابع را برای نقطه‌ای مانند ${\displaystyle {\begin{alignedat}{2}x_{0}\end{alignedat}}}$می‌گیریم. سپس برای تابع $f'$ریشه را به دست می‌آوریم. ریشه نقطه‌ای مانند $x_{1}$می‌شود سپس برای نقطهٔ $x_{1}$از تابع $f$مشتق می‌گیریم و ریشهٔ این معادلهٔ به دست آمده به عنوان $x_{2}$ما انتخاب می‌شود و همین روال به صورت تکراری ادامه خواهد داشت.

برای درک بهتر به تصویر زیر توجه کنید:

روش وتری

از آنجائیکه روش‌های دو بخشی و نابجایی با سرعت کمی به سمت ریشه میل می‌کنند، لذا شیوه ای سریعتر برای یافتن ریشه نیاز است. یک چنین شیوه ای، روش وتری نام دارد. مشابه شیوهٔ نابجایی ، اساس این روش نیز بر تقریب زدن ریشه تابع از طریق یک خط مستقیم قرار دارد که دو نقطه از نمودار تابع را به یکدیگر وصل می‌کند، اما نیازی نیست که نقاط حدس اولیه حتماً دارای عالمت مخالف باشند.

• گام اول:$x_{i+1}=x_{i}-{{{f(x_{i})}(x_{i-1}-x_{i})} \over f(x_{i-1})-f(x_{i})}$
• گام دوم:$e_{n}=|x_{i+1}-x_{i}|\leqslant \epsilon _{i}\quad and/or\quad e_{n}=|f(x_{i+1})|\leqslant \epsilon _{2}$
• گام سوم: اگر شرط فوق برقرار باشد، به مرحله چهار برو، در غیراینصورت داریم:$set\quad x_{i}=x_{i+1},x_{i-1}=x_{i}$
• گام چهارم :نمایش $x_{i+1}$به عنوان ریشه و پایان الگوریتم.

یک شبه کد برای این الگوریتم:$$The\ Secant\ Method$$$$Given\ f(x)\ =0\,\epsilon \ and\ two\ initial\ points\ x_{0},x_{1};$$$$Given\ max\ =maximum\ number\ of\ iterations;$$$$For\ i=1\ to\ max:$$$$compute\ \ g'(x_{i})={{{f(x_{i})}-(x_{i-1})} \over x_{i}-x_{i-1}};$$$$compute\ \ x_{i+1}=x_{i}-{f(x_{i}) \over g'(x_{i})};$$$$If\ |x_{i+1}-x_{i}|<\epsilon :$$$$Solution=x_{i+1};$$$$stop\ the\ iterations;$$$$endif$$$$endfor$$